Perfect Info About How To Interpret Line Fit Plots Excel Graph Generator

This short minitab video demonstrates how to complete the fitted line plot example from the 'lean six sigma and minitab' guide, published by opex resources.w.

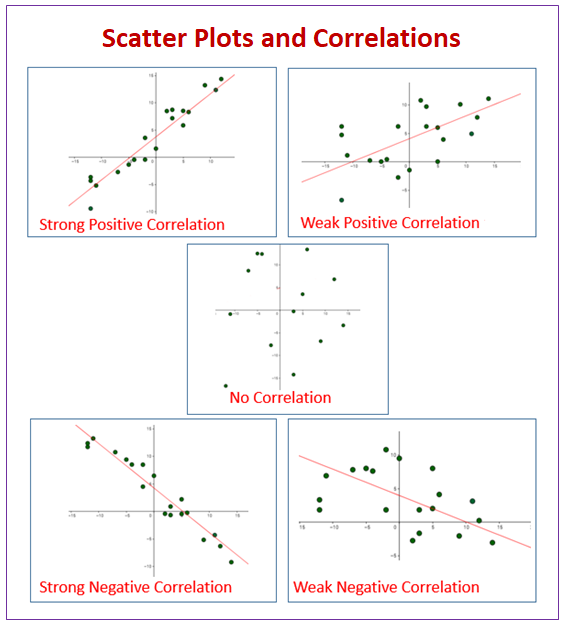
How to interpret line fit plots. Under residual plots, select four in. Examine the fitted line plot to determine whether the following criteria are met: The sample contains an adequate number of observations throughout the entire range of all the predictor values.

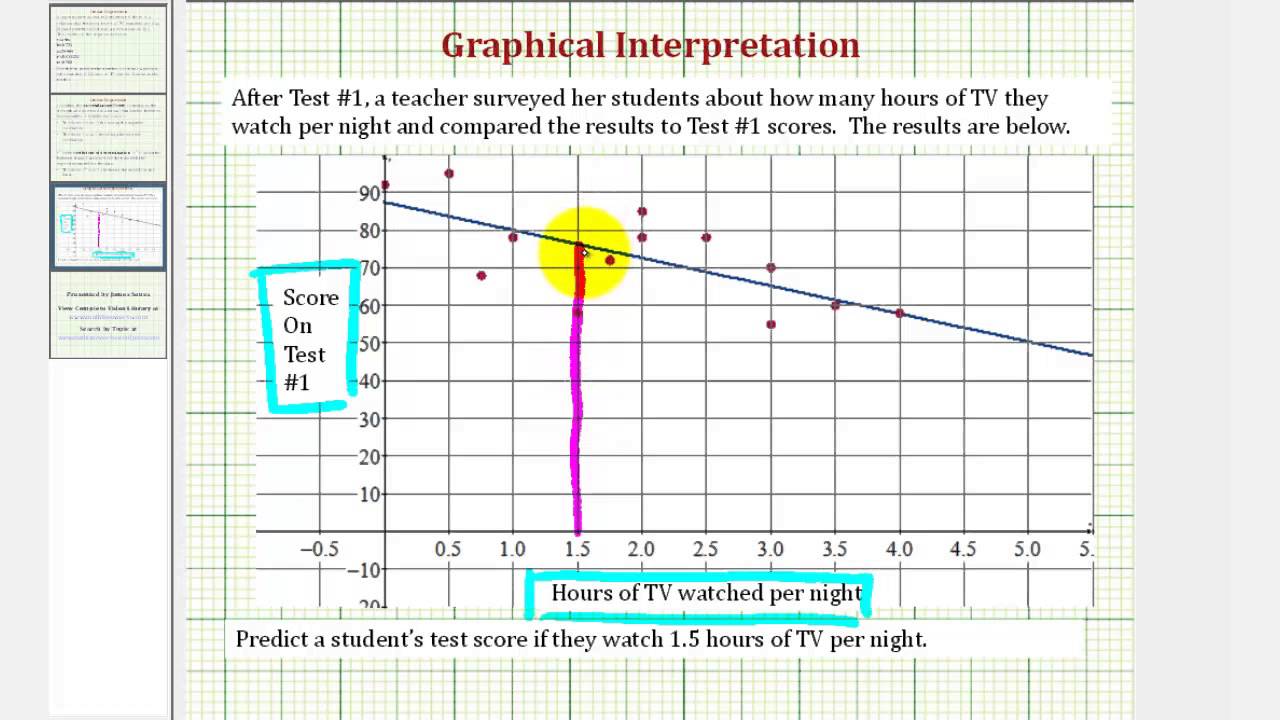
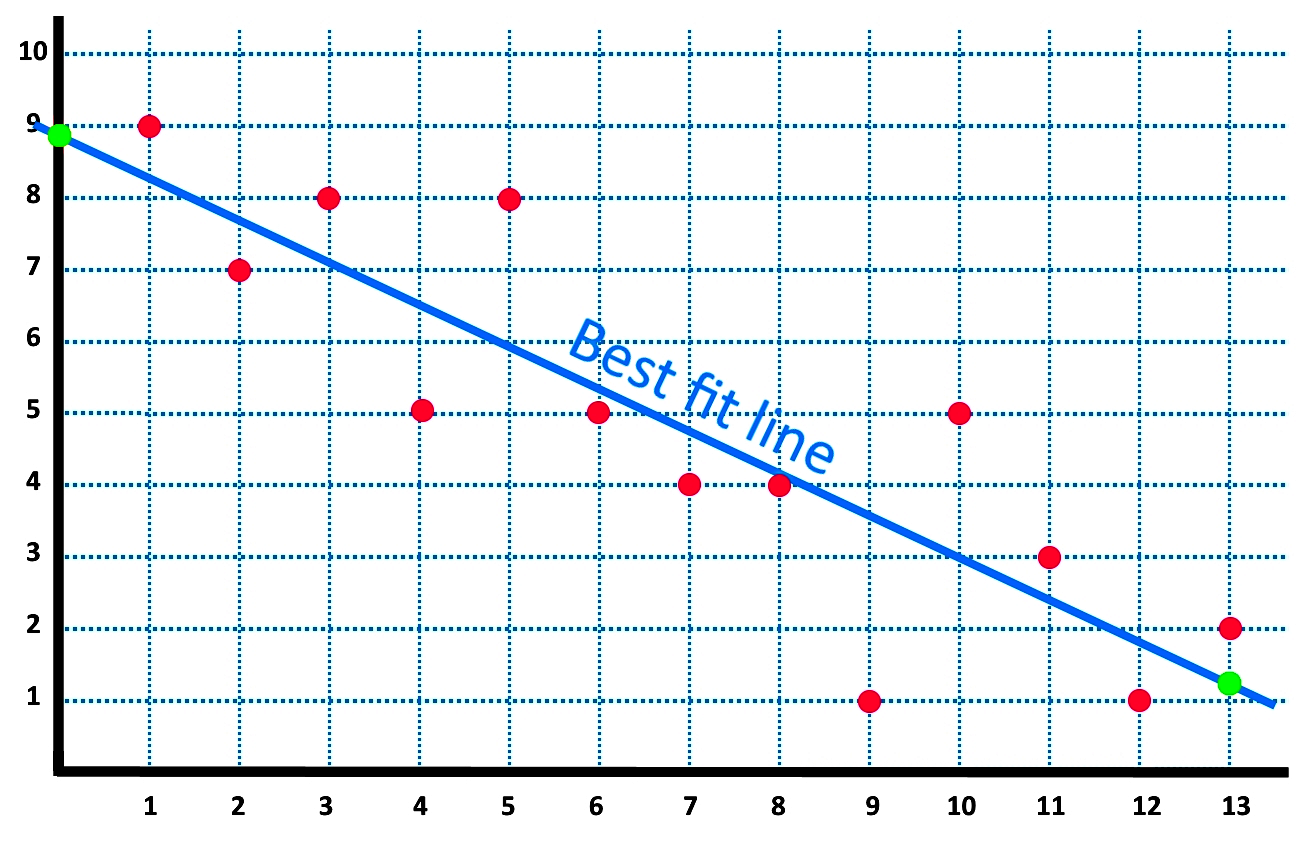
The closer the points are to the line of best fit the stronger. That is, the residuals are close to 0 for small x values and are more spread out for large x values. The relationship between their ratings and the price of the chips is shown in the scatter plot below.

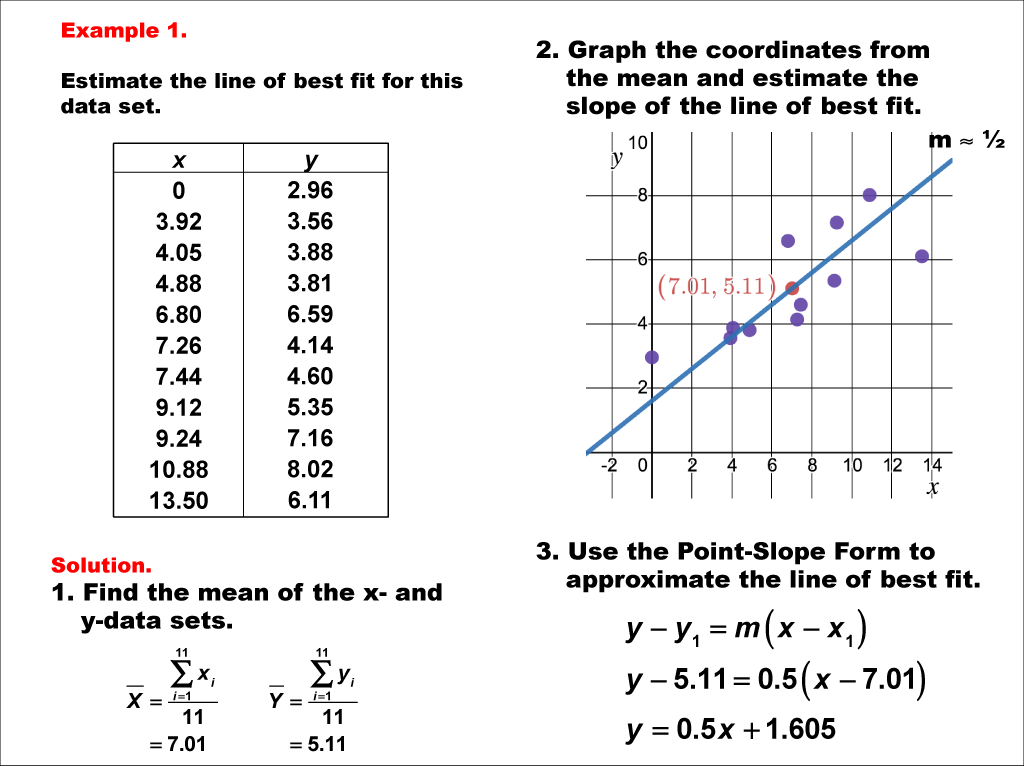
The plot has a . First, look at your ordered pairs and find the mean of all of the x values and all of the y values. When conducting a residual analysis, a residuals versus fits plot is the most frequently created plot.

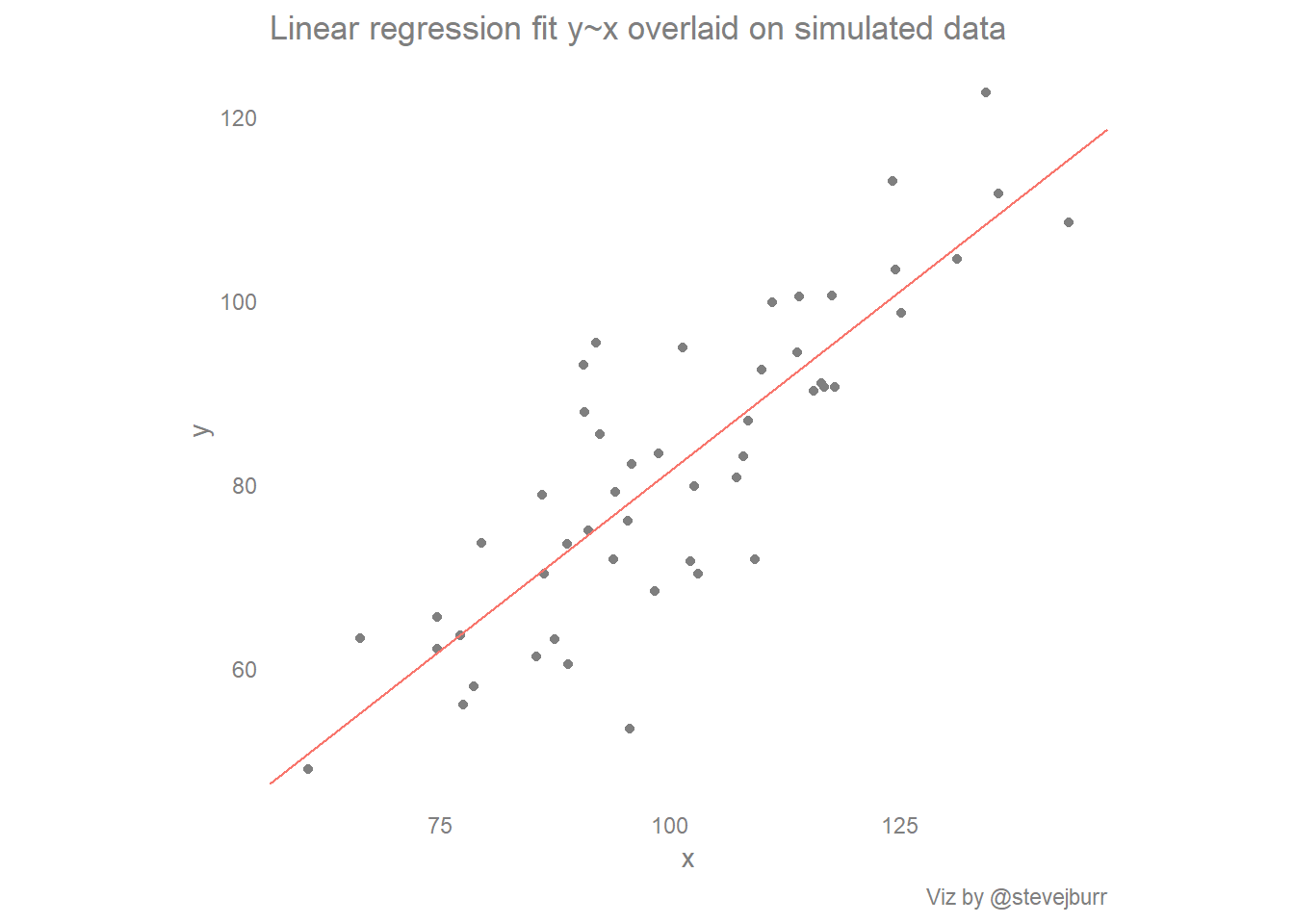
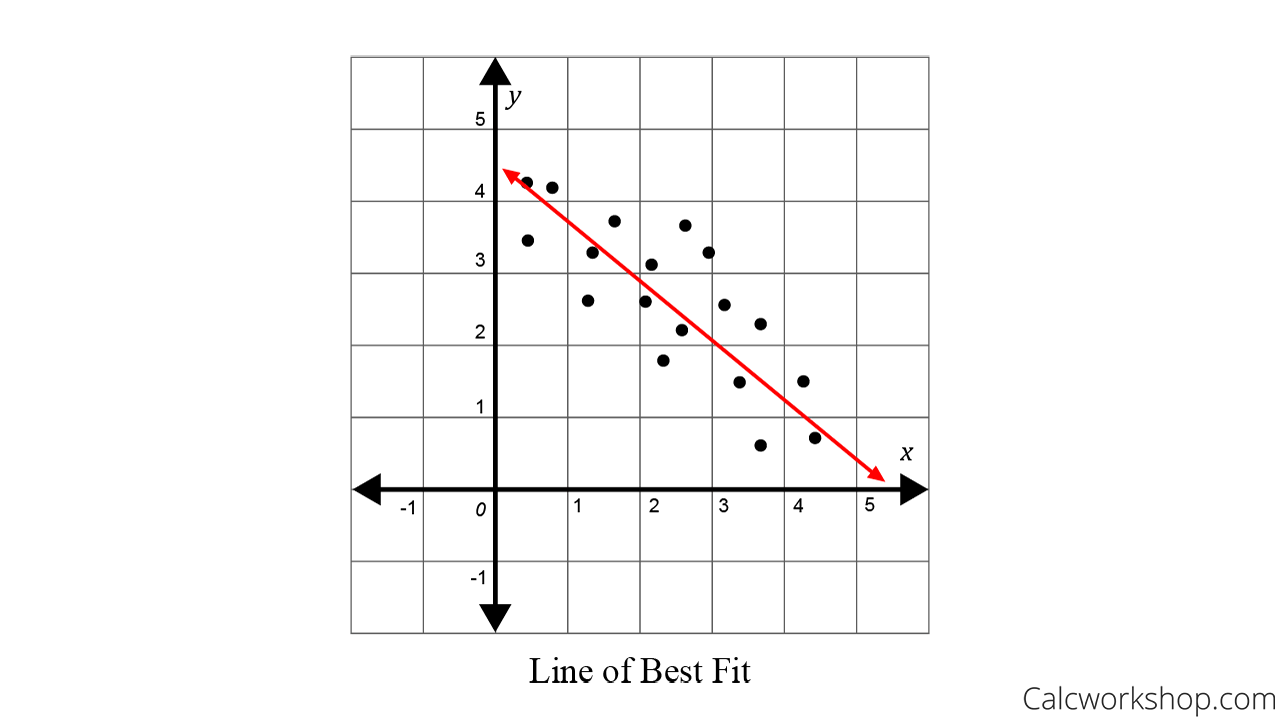
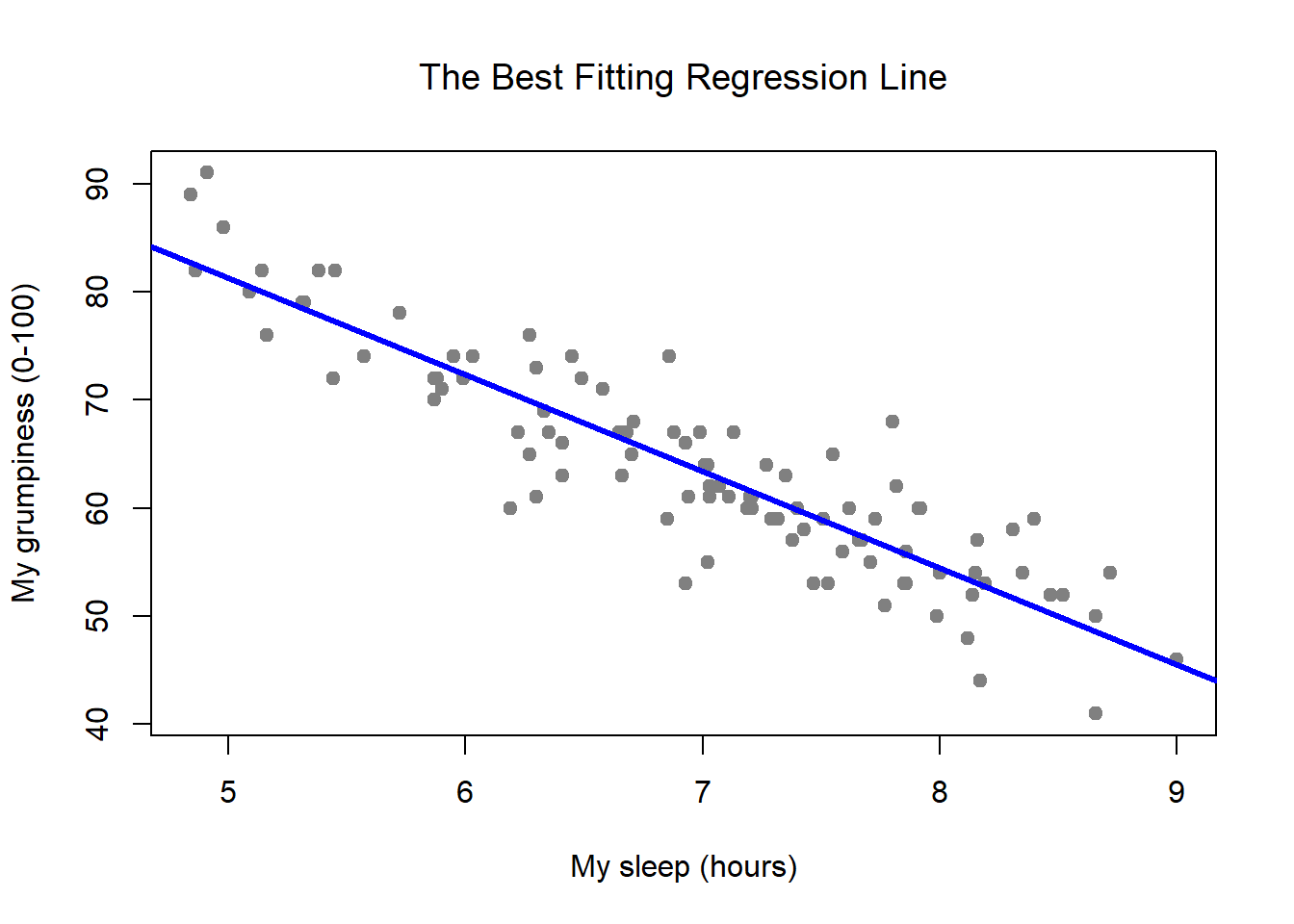
Evaluate how well the model fits your data and whether the model meets your goals. A fitted line plot of the resulting data, ( alcohol arm data ), looks like this: The line of best fit (or trendline) is an educated guess about where a linear equation might fall in a set of data plotted on a scatter plot.

You can fit a linear, quadratic, or cubic model to the data. Beginning with straight lines; It also suggests that there are no unusual data points in the data set.

The line of best fit is used to express a relationship in a scatter plot of different data points. Open the sample data, particleboard.mtw. Use these plots to assess model fit by comparing how well the fitted values follow the observed values.

It is an output of regression analysis and can be used as a prediction tool for indicators and. Under type of regression model, select quadratic. The p value is the probability of finding the observed results when.

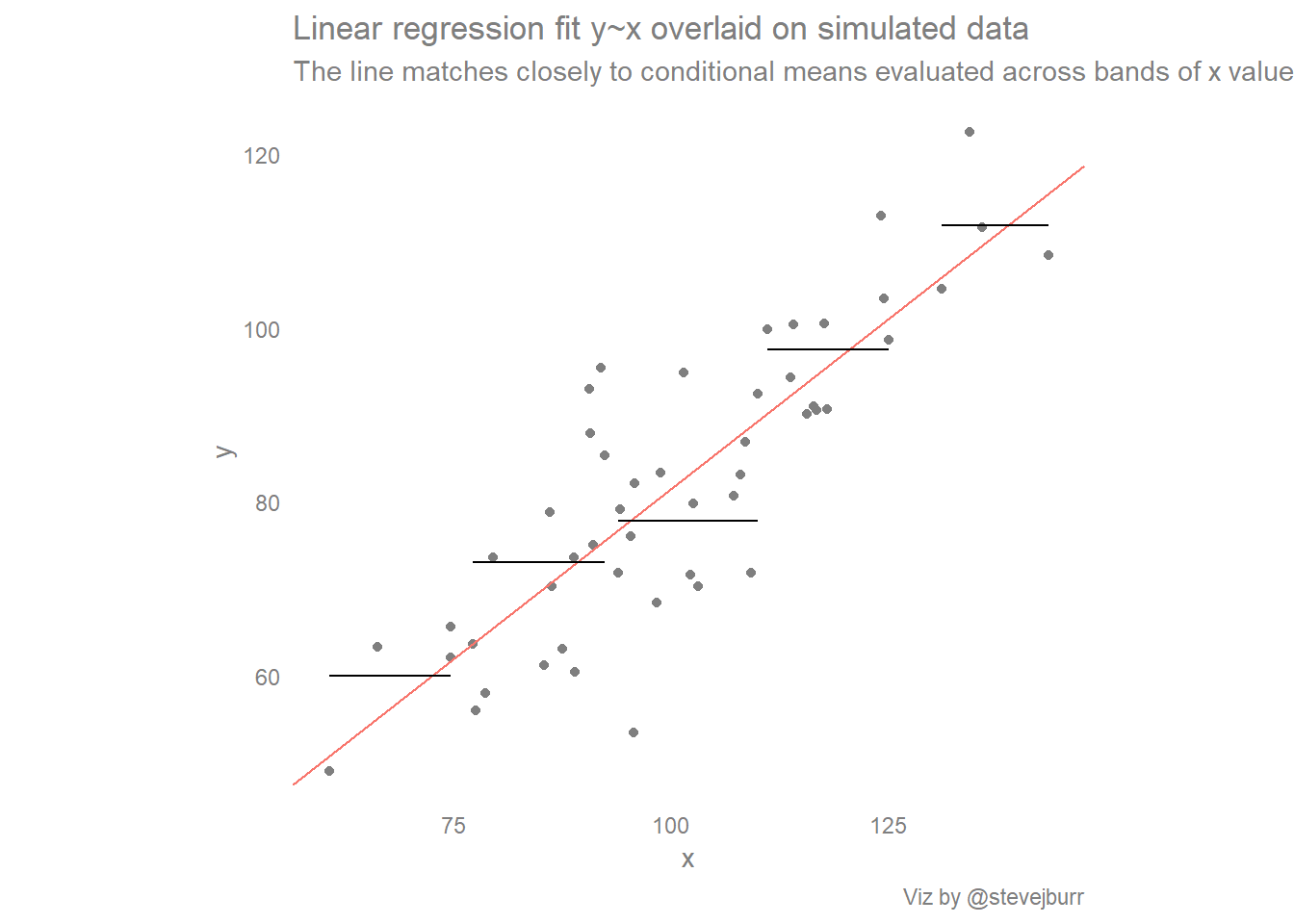
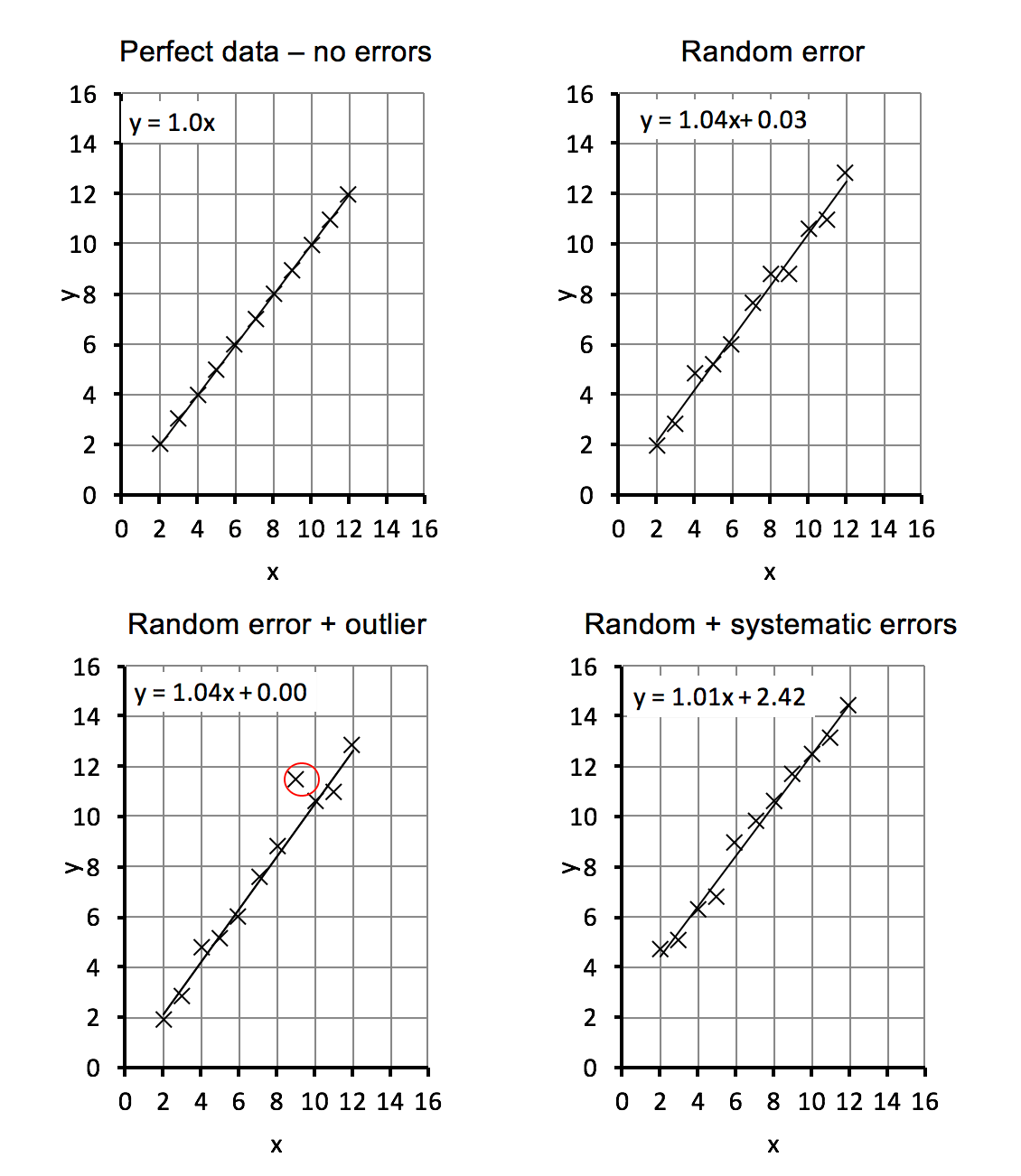
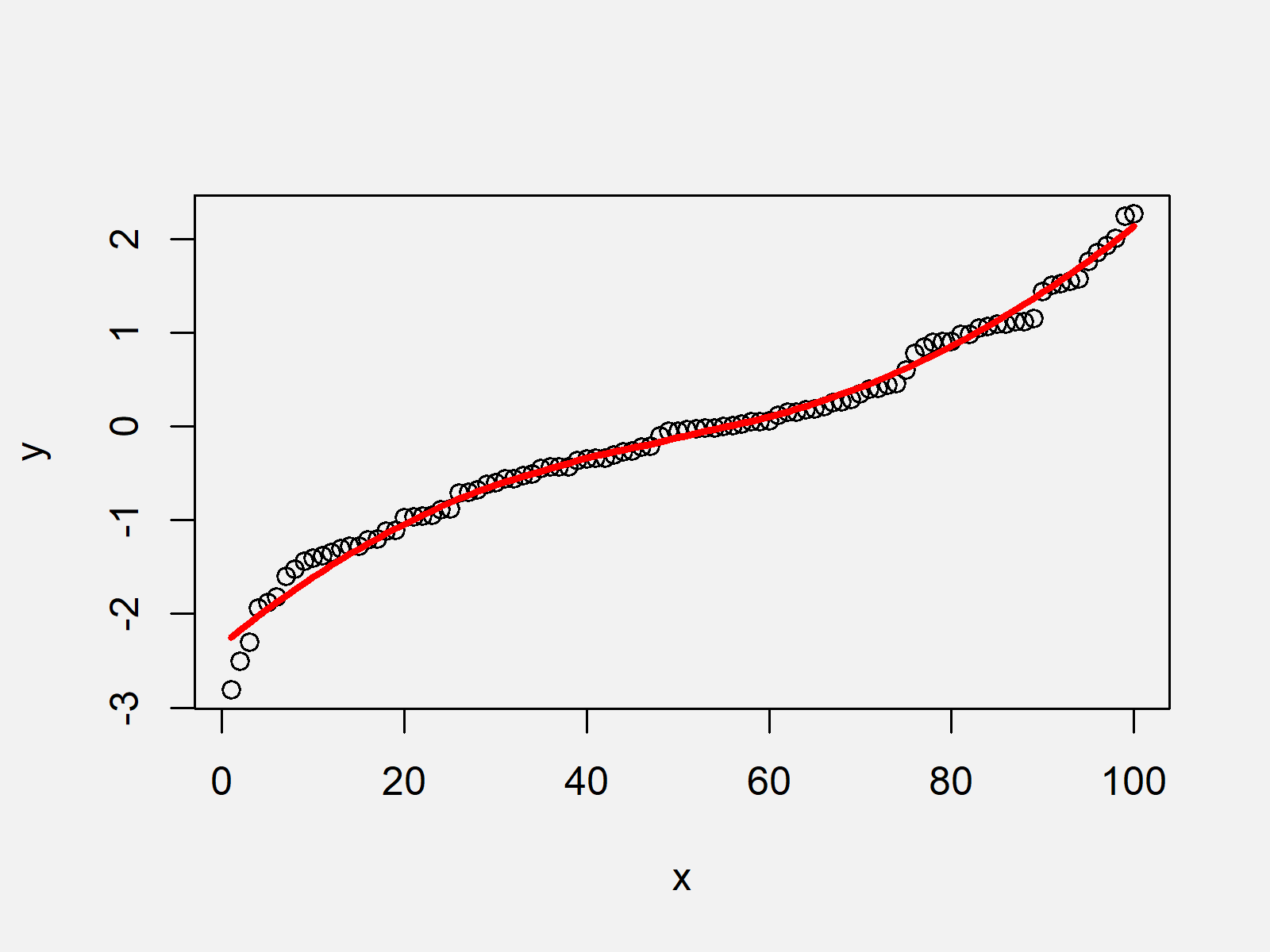
In a “good” residual plot, the residuals are randomly scattered about zero with no systematic increase or decrease in variance. In general, we fit lines to data when we want to use them for predictive purposes or to determine the general trend of the data. In a “bad” residual plot, the variance of the residuals increase or decrease in a systematic way.

The fitted line plot command is one way of obtaining the estimated regression function between a response y and a predictor x. Do the residuals increase or decrease in variance in a systematic way? It is a scatter plot of residuals on the y axis and fitted values (estimated responses) on the x axis.

The fitted line plot command provides not only the estimated regression function but also a scatter plot of the data adorned with the estimated regression function. The plot has a fanning effect. Consider the following figure from faraway's linear models with r (2005, p.