Marvelous Info About Is A Straight Line Smooth Function Adding Trendline To Excel Chart

Using friedrichs mollifiers you are able to construct smooth functions which are identically one, hence with second derivative identically $0$, in a neighborhood of any compact set.

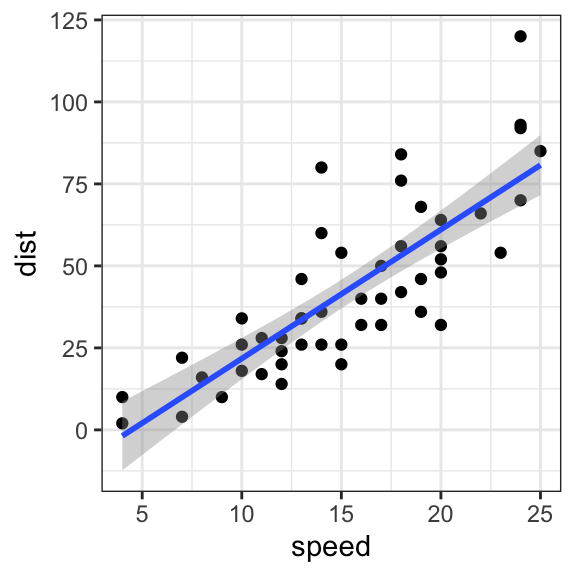
Is a straight line a smooth function. The function $h(x)=0$ is differentiable with $h'(x)=0$. Tangent vector if γis a parametrized. A straight line suggests that the value between the two measurements increased linearly, while a curved line suggests otherwise.

An antiderivative of such a function instead connects two lines with different slope (zero. Generalized linear models to include smooth functions of explanatory variables with the smoothness determined by either a parameter that directly controls the smoothness of. For a relation to be a function, use the vertical line test:

\(\vecs r\) is not smooth at \(t = 0\) and \(t = 2\), since \(\vecs r'(0) = \vecs 0\) and \(\vecs r'(2) = \vecs 0\). Smooth function a function f: Draw a vertical line anywhere on the graph, and if it never hits the graph more than once, it is a function.

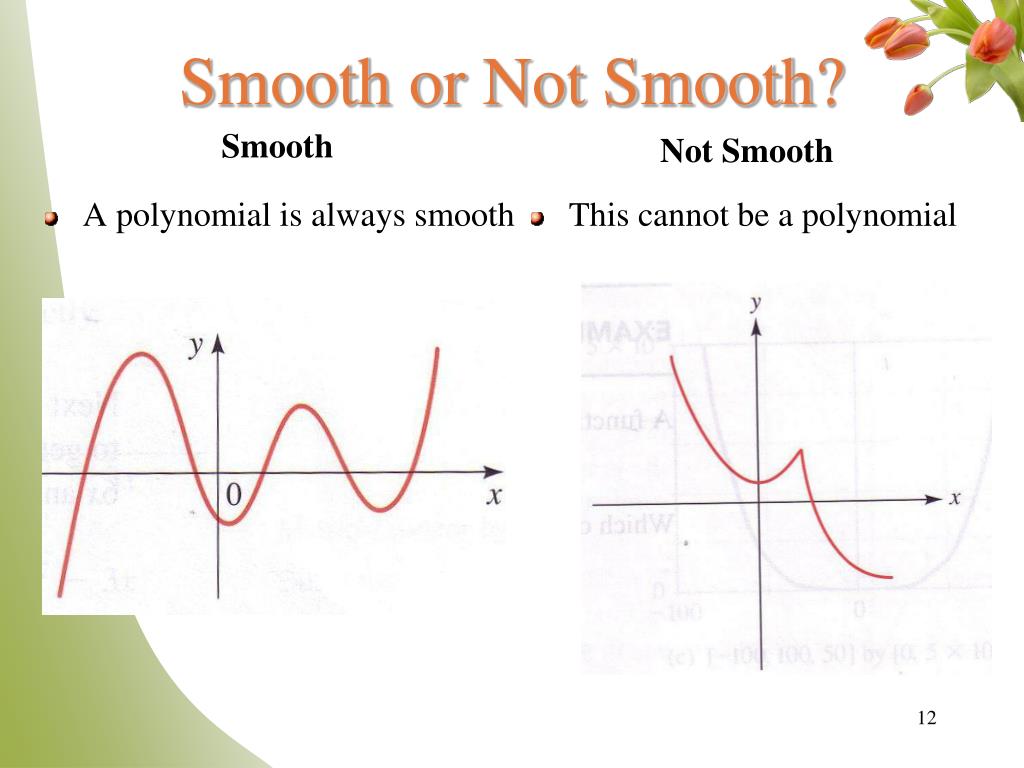
A function can therefore be said to be smooth over a. A smooth function can refer to a function that is infinitely differentiable. So yes your function is smooth.

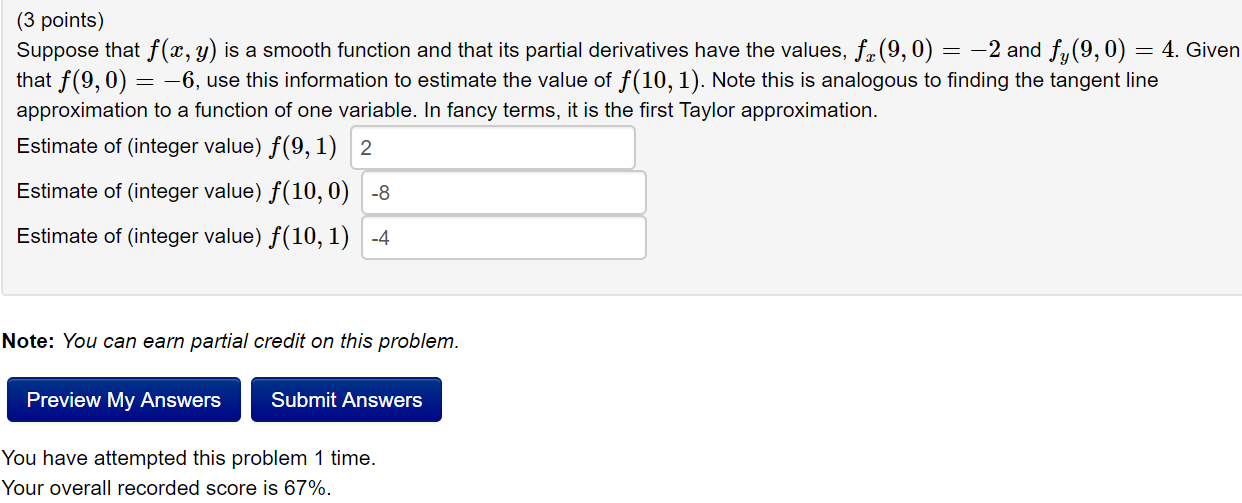
As long as x =0, the graph of f(x) has a well defined tangent line at the point (x, f(x)). Now i want a smooth curve to go through. But in the technical sense, the function above is infinitely smooth and infinitely differentiable.

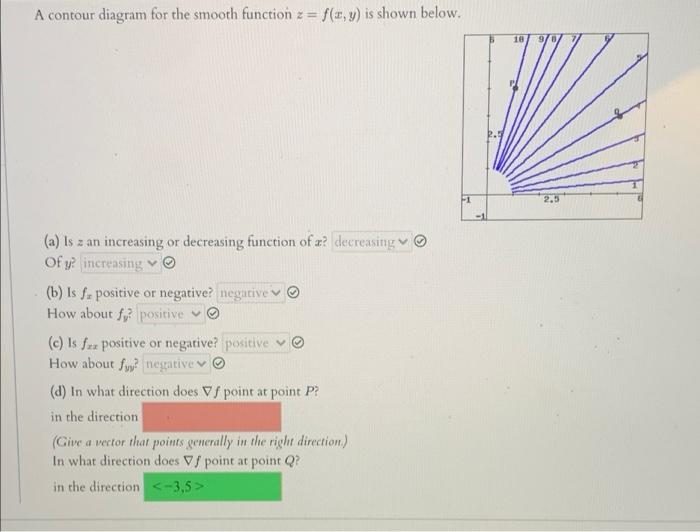
To the left, the graph is a smooth curve. In particular, a smooth curve is a. (α,β) →r is said to be smooth if the derivative dnf dtn exists for all n≥1 and all t∈(α,β).

X = 0, the graph of f(x) is a straight line. I'm looking for a way to define some sort of a smoothness value for each point on a line. Note that in some contexts smooth can mean different things, such as 1 or 2 times.

Then i would in turn define the smoothness of a closed loop to be the. It connects two lines smoothly, but both lines have zero slope. No matter what you choose,.

There's no way to smooth that data reliably without providing more information about the time effect. In matlab, ultimately every curve is approximated by straight lines or discretized into pixels. A smooth function is just like the name sounds:

A straight line that passes through a speci c point has a direction, or slope, that characterizes it. In mathematical analysis, the smoothness of a function is a property measured by the. A smooth curve is a curve which is a smooth function, where the word curve is interpreted in the analytic geometry context.