Stunning Info About What If Two Lines Are Parallel On A Graph Difference Between Dual Axis And Blended In Tableau

Y = mx + b.

What if two lines are parallel on a graph. How do you tell if two lines are parallel, perpendicular, or neither? Their slopes are the same! Created by sal khan and monterey institute for technology and education.

We know that parallel lines have the same slope. Two lines are parallel if their graphs never intersect. If the slope values are equal (m = n), then the lines are.

Parallel lines cut by a transversal have the following properties: 2 4 6 8 − 4 − 6 − 8 2 4 6 8 − 4 − 6 − 8 y x a b. Parallel lines are lines that never intersect, and they form the same angle when they cross another line.

If the slopes are different, the lines are not parallel. And passes though the point (5,4) the slope of y = 2x + 1 is 2. We can identify these lines using angles and symbols in diagrams.

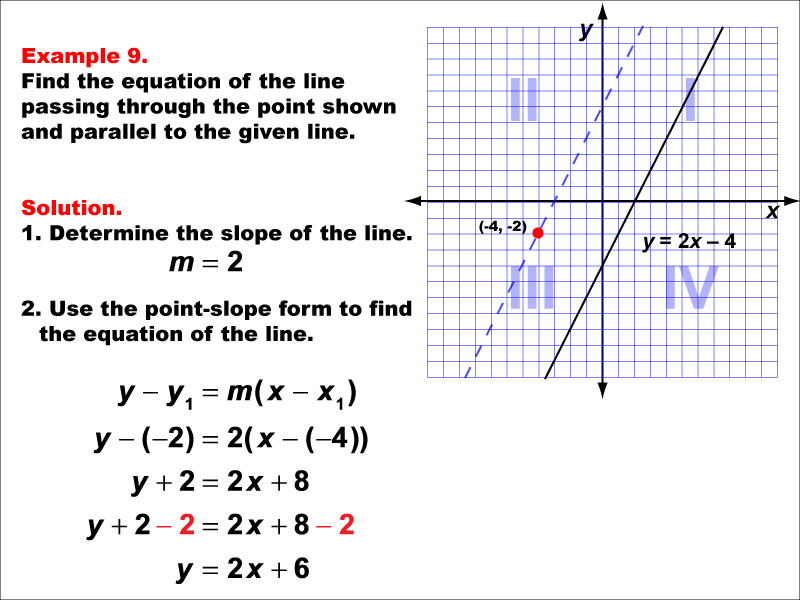
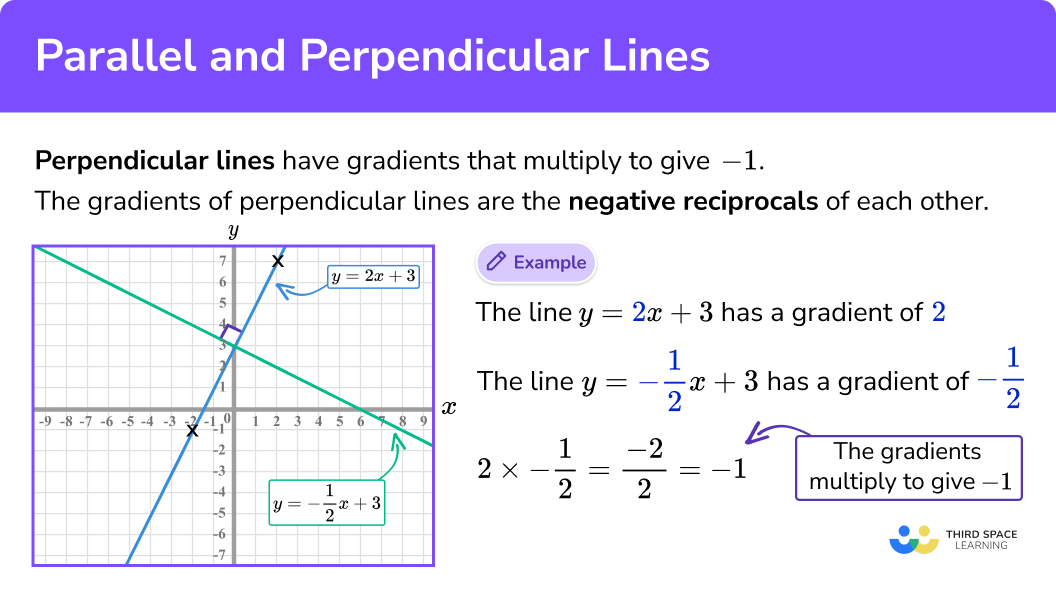
The parallel line needs to have the same slope of 2. Suppose two lines are given: The slope of one line is the negative reciprocal of the other.

So this line right over here and this line right over. We’ll use the notation m∥m∥ to represent the slope of a line parallel to a line with slope m. I need help with finding the equation of a line parallel to another line.

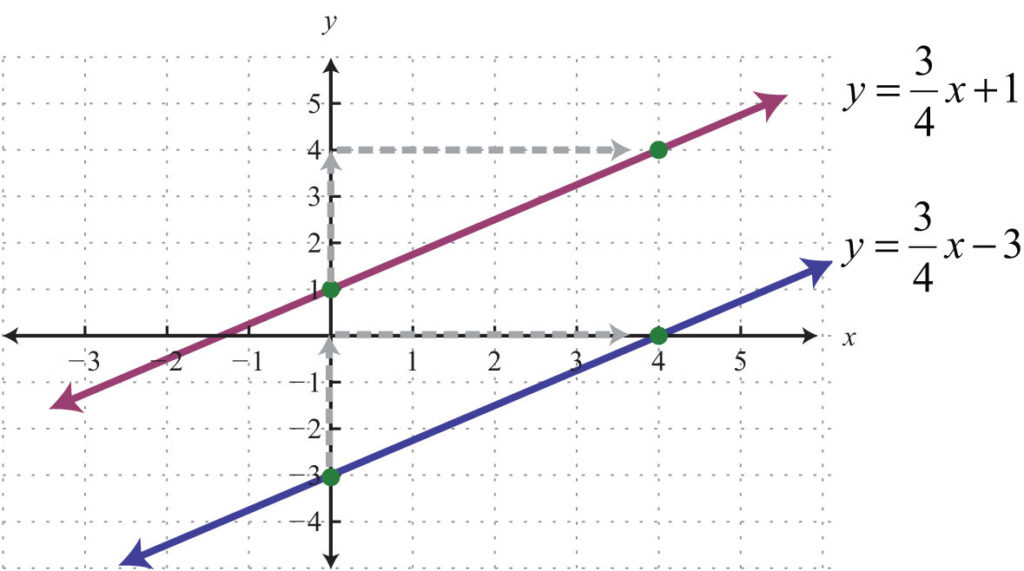
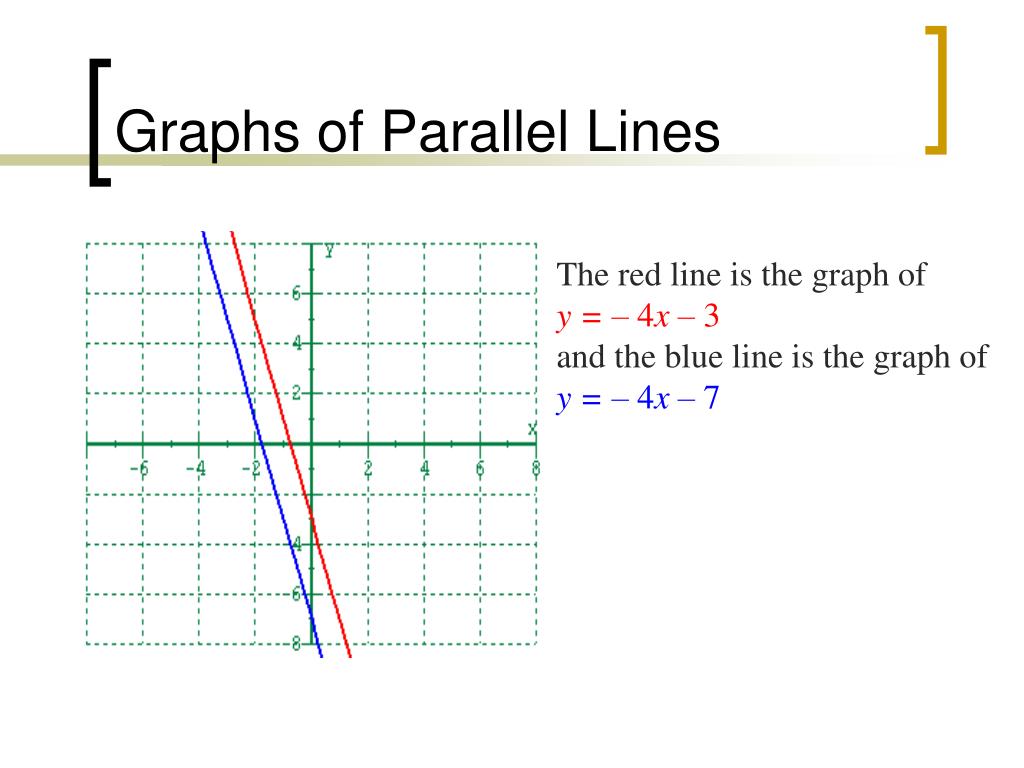
Parallel to y = 2x + 1. State the equation of a line that is parallel to \ (y = 3x + 7\). Here are the two examples of parallel line pairs when they are graphed.

If two lines are parallel to the same line, they are parallel to each other. They can be both horizontal and vertical. Two nonvertical lines in the same plane, with slopes \(m_{1}\) and \(m_{2}\), are parallel if their slopes are the same, \(m_{1}=m_{2}\).

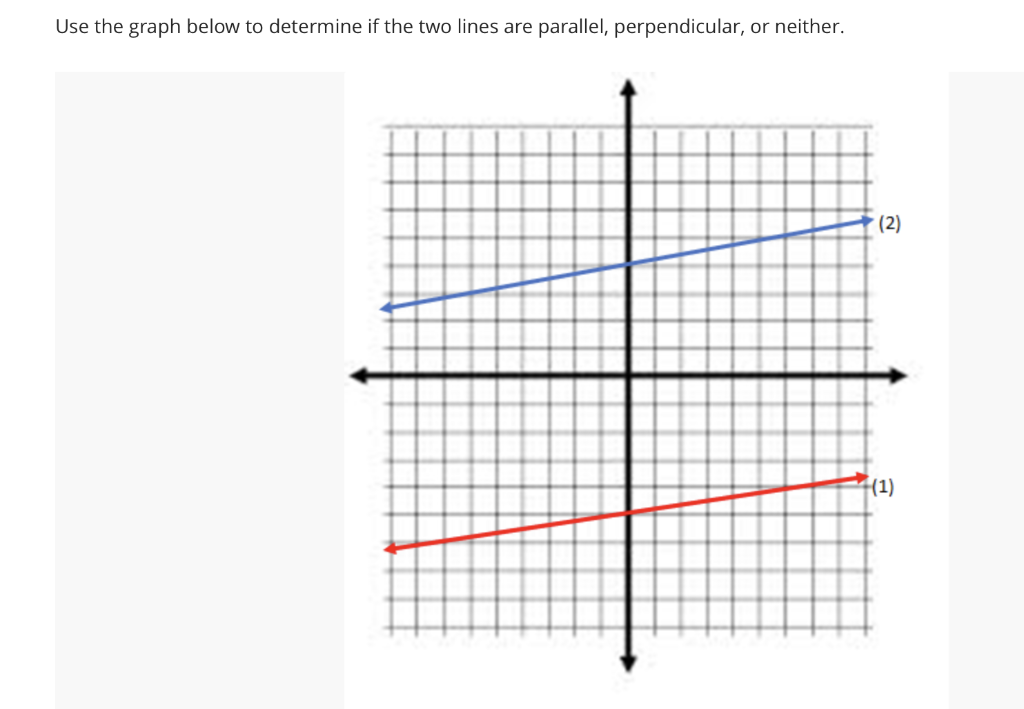
How do we know when two lines are parallel? This is a worked example of determining whether given lines are parallel or perpendicular. Consider the following two lines:

Want to join the conversation? Graph the two lines and determine whether they are parallel, perpendicular, or neither: Sal determines which pairs out of a few given linear equations are parallel.